FUNGSI KOMPOSISI & FUNGSI INVERS
1.1 Relasi
Misal A dan B adalah himpunan. Jika anggota A dikaitkan dengan anggota B berdasarkan suatu hubungan tertentu maka akan terdapat suatu relasi A dan B. Relasi tersebut dapat dinyatakan dengan R : A B
B
Contoh
A = { 1, 2, 3, 4 } dan = { 1, 2, …. 6 }
Misal relasi dari A ke B adalah searah dari, maka relasi tersebut dapat digambarkan seperti digambarkan diagram disamping.
1.2 Fungsi atau Pemetaan
Suatu relasi dari A ke B yang memasangkan setiap anggota A dengan tepat satu anggota kecil. Misalnya f adalah fungsi dari A ke B, fungsi ini ditulis dengan f : A B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).
B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).
Jika f memetakan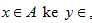 maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x
maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x y atau y = f (x). Himpunan
y atau y = f (x). Himpunan  yang merupakan peta dari
yang merupakan peta dari  disebut range atau daerah hasil.
disebut range atau daerah hasil.

 1.3 Komposisi Fungsi
1.3 Komposisi Fungsi
Penggabungan operasi dan fungsi secara berurutan akan menghasilkan sebuah fungsi baru. Penggabungan tersebut disebut komposisi fungsi dan hasilnya disebut fungsi komposisi. Perhatikan diagram berikut!
Pada diagram di atas fungsi f di komposisikan sebagai fungsi g yang mengahasilkan fungsi h . h adalah fungsi komposisi dari t dan g dinotasikan dengan


1.4 Invers Fungsi
Misal fungsi f : A B maka invers fungsi f dinyatakan dengan
B maka invers fungsi f dinyatakan dengan  Jika y = f (x) maka
Jika y = f (x) maka 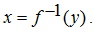
Contoh :
Tentukan invers fungsi
a. f (x) = 2 x + 6
misalnya :
y = 2x +6
 2x = y-6
2x = y-6 

Dengan demikian :

Cara lain :


1.5 Invers fungsi Komposisi Misal fungsi f : A B dan g : B
B dan g : B  C. Jika h adalah fungsi komposisi dari f atau g .
C. Jika h adalah fungsi komposisi dari f atau g .  dengan
dengan  maka invers fungsi fungsi h adalah
maka invers fungsi fungsi h adalah  dengan
dengan  jadi jika
jadi jika  maka
maka 
Misal A dan B adalah himpunan. Jika anggota A dikaitkan dengan anggota B berdasarkan suatu hubungan tertentu maka akan terdapat suatu relasi A dan B. Relasi tersebut dapat dinyatakan dengan R : A
 B
B Contoh
A = { 1, 2, 3, 4 } dan = { 1, 2, …. 6 }
Misal relasi dari A ke B adalah searah dari, maka relasi tersebut dapat digambarkan seperti digambarkan diagram disamping.
1.2 Fungsi atau Pemetaan
Suatu relasi dari A ke B yang memasangkan setiap anggota A dengan tepat satu anggota kecil. Misalnya f adalah fungsi dari A ke B, fungsi ini ditulis dengan f : A
 B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).
B. Dalam hal ini A disebut Domain ( daerah asal dan B disebut Kodomain (daerah kawan).Jika f memetakan
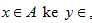 maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x
maka dapat dinyatakan bahwa y adalah peta dari x dan hal ini dapat dituliskan dengan f : x y atau y = f (x). Himpunan
y atau y = f (x). Himpunan  yang merupakan peta dari
yang merupakan peta dari  disebut range atau daerah hasil.
disebut range atau daerah hasil.
 1.3 Komposisi Fungsi
1.3 Komposisi FungsiPenggabungan operasi dan fungsi secara berurutan akan menghasilkan sebuah fungsi baru. Penggabungan tersebut disebut komposisi fungsi dan hasilnya disebut fungsi komposisi. Perhatikan diagram berikut!

Pada diagram di atas fungsi f di komposisikan sebagai fungsi g yang mengahasilkan fungsi h . h adalah fungsi komposisi dari t dan g dinotasikan dengan



1.4 Invers Fungsi
Misal fungsi f : A
 B maka invers fungsi f dinyatakan dengan
B maka invers fungsi f dinyatakan dengan  Jika y = f (x) maka
Jika y = f (x) maka 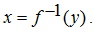
Contoh :
Tentukan invers fungsi
a. f (x) = 2 x + 6
misalnya :
y = 2x +6
 2x = y-6
2x = y-6 

Dengan demikian :


Cara lain :


1.5 Invers fungsi Komposisi Misal fungsi f : A
 B dan g : B
B dan g : B  C. Jika h adalah fungsi komposisi dari f atau g .
C. Jika h adalah fungsi komposisi dari f atau g .  dengan
dengan  maka invers fungsi fungsi h adalah
maka invers fungsi fungsi h adalah  dengan
dengan  jadi jika
jadi jika  maka
maka 
Tidak ada komentar:
Posting Komentar